Некоторые системы символьных вычислений
с открытым кодом

А.В. Цыганов, физический факультет СПбГУ, 2007.

Системы символьных вычислений сегодня активно используются в различных областях знаний, в том числе и в математике. Наиболее яркие примеры использования таких систем в ”чистой” математике – доказательство в 1976 гипотезы о четырехцветном раскрашивании, доказательство гипотезы Кеплера, формулировка и доказательство гипотез Birch and Swinnerton-Dyer.

По статистическим данным, по результатам публикаций в американских математических журналах за 2007 год, при доказательстве одного математического утверждения - математиками, физиками, химиками и т.д. – использовалось в среднем по три различных программы символьных вычислений. (Максимальное число было шесть программ!) Некоторые из них были достаточно узко специализированными программами, некоторые более универсальными и претендующими на всеобщность системами компьютерной алгебры. Конечно же, среди них были и коммерческие программы, такие как MatLab, Mathematica и Maple.

В качестве примера: система CoCoA (http://cocoa.dima.unige.it/flyer4.html) специально разработана для работы с полиномами. Я ее активно использую для нахождения специальных полиномиальных соотношений – сизигий – над кольцом полиномов. Некоторые из тех же самых сизигий можно достаточно просто найти и в системе Maple, однако возможности и эффективность работы специализированной системы системы CoCoA существенно выше. В некоторых случаях система Maple не может получить соотношения, получаемые в CoCoA, хотя затем и способна проверить уже полученные соотношения. Естественно, интерфейс и удобство работы с системами с открытым кодом пока еще существенно ниже по сравнению с коммерческими системами – но эти неудобства любой ученый с радостью обменяет на возможность получения нового результата!

Итак, после широкой и продолжительной дискуссии в математическом сообществе на Западе сформировалась следующая точка зрения:

Результат, полученный с помощью систем символьных вычислений с закрытым кодом, не может считаться частью математического доказательства, так как сам код проверить невозможно.

Верное и обратное,

Результат, полученный с помощью систем символьных вычислений с открытым кодом, считается доказанным.

Более подробное обсуждение этой философии, со всеми необходимыми ссылками, может быть найдено здесь.

Далее мы перечислим несколько программ, которые удовлетворяют условию открытости кода, и добавим маленький комментарий к ссылкам. К сожалению, более подробное описание каждой из программ не входит в наши цели. Некоторые из этих проектов активно развиваются, некоторые находятся в ”временной” стагнации, некоторые уже почти закончили свой жизненный цикл.

·         SAGE ("Software for Algebra and Geometry Experimentation") – наиболее агрессивно развивающийся проект, который уже ”съел”, в хорошем смысле этого слова, проекты Axiom, GAP, GP/PARI, Macaulay2, Maxima, Octave, Singular и некоторые другие.

На сайте проекта  можно найти следующую картину ”великого объединения” open-source проектов по различным разделам математики:

Algebra and calculus

Maxima, Sympy

Arbitrary precision arithmetic

GMP, MPFR, MPFI, NTL, quaddouble, Givaro

Algebraic geometry

Singular, Macaulay2

Arithmetic Geometry

PARI, NTL, mwrank, ecm, FLINTQS

Exact linear algebra

Linbox, IML

Graphics

MatPlotLib, Tachyon3d, Java3d, VTK (optional)

Group theory

GAP

MATLAB-like functionality – linear algebra, optimization

GSL, Scipy, Numpy

Последняя версия SAGE 2.10.1 была реализована 8 февраля 2008 года. Работает под Windows, Mac OS X и Linux. Распространяется по условиям GNU General Public License лицензии. Лидер команды разработчиков  William Stein.

Одной из отличительных черт этого пакета является использовании языка Python, число пользователей которого приближается к нескольким миллионам. К сожалению, у нас нет возможности поговорить об этом языке, который очень интересен – например очень большая часть движка Google написана именно на нем. Описание языка можно посмотреть здесь.

Пример работы с SAGE из документации на сайте



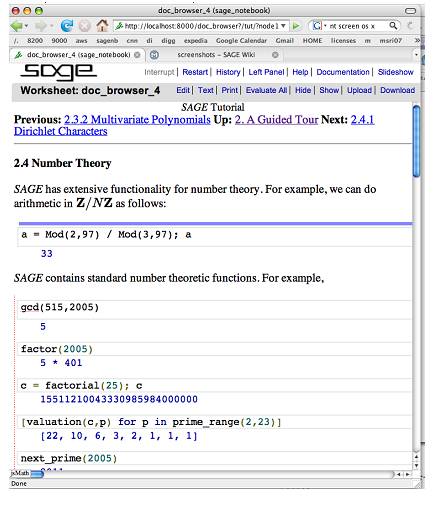
Первые версии SAGE, написанные на C++, мне так и не удалось запустить, но после перехода на Python в 2005 году все стало работать и в настоящее время пакет производит очень хорошее впечатление и по возможностям и по интерфейсу.

Более подробно мы не будем подробно описывать этот амбициозный проект, так как мы переходим к разговору о тех проектах, которые в настоящее время уже стали ”частью” SAGE

       В качестве примера приведу кусочек программы для Axiom, который иллюстрирует теорему Ферма:

-- run in axiom(1) with the command

-- )read fermat.little.axiom.input

)clear all

topprimetotest: Integer := 341

topintegerbasetotest: Integer := 10

n: Integer := 340

x: Any

repeat

if n = topprimetotest then break

a: Integer :=2

n := n+1

repeat

if (a >= n) or (a > topintegerbasetotest) then break

-- If the 2nd and 4th fields are unequal, n is composite.

-- By Fermat’s little theorem: n prime, then n divides a^n - a

-- Carmichael numbers are composite but pass this prime test

-- e.g., 561, 1105, 1729

x := a^n

output [n,a,x,x:: IntegerMod(n)]

if a ~= x:: IntegerMod(n) then break

a := a+1

factor(341)

·         Maxima - система компьютерной алгебры, которая используются для различных исследований, прародителем этой системы был проект DOE Macsyma, который начал свое существование в 1960s в MIT и который можно считать прародителем также и систем Maple и Mathematica. С 1998 распространяется по условиям GNU General Public License лицензии. Мне лично этот пакет не очень нравится, так как он все же слишком близок по духу к коммерческим продуктам Maple и Mathematica, но сильно им уступает и по возможностям и по реализации.

·         GAP – позиционируется разработчиками как система дискретной алгебры. Очень удобна и эффективны , по моему собственному опыту, при вычислениях, которые возникают в теории групп и представлений, работе с кольцами, векторными пространствами, в комбинаторике и т.д. . GAP представляет пользователю собственный язык, огромную библиотеку собственных программ и баз данных математических объектов с заданными. Распространяется по условиям GNU General Public License лицензии.

·         GINAC ("Ginac Is Not A Cas") – этот специализированный пакет интересен тем, что использует язык C++, дополняя его необходимыми встроенными процедурами – детали могут быть найдены здесь. Распространяется по условиям GNU General Public License лицензии.

·       Macaulay2 – специализированная система для исследований в области алгебраической геометрии и коммутативной алгебры. Распространяется по условиям GNU General Public License лицензии, версии 2.

·         PARI/GP – очень широко распространенная система компьютерной алгебры, которая базируется на самых современных алгоритмах и очень эффективна для вычислений в теории чисел (факторизация, алгебраическая теория чисел, эллиптические кривые и т.д.), к этому надо добавить огромное число и других встроенных функций и процедур. Очень быстрая и при этом достаточно неприхотливая система. Распространяется по условиям GNU General Public License лицензии.

·         The Magnus Computational Group Theory Package – предназначен в основном для работы с бесконечными группами и их представлениями. Как я понял, глядя на документацию разработчиков, распространяется по условиям GNU General Public License лицензии, версии 2. Очень специализированный пакет, в котором мне, как не специалисту, так и не удалось ничего посчитать!

·         GNU Octave – разрабатывался как язык высокого уровня для численных вычислений. В настоящее время работа с ним состоит из введения команд в режиме командной строки , которые позволяют численно линейные и нелинейные уравнения. Синтаксис в основном полностью совпадает с синтаксисом системы MatLab, но возможности конечно несопоставимы.

·         R Project for Statistical Computing – система символьных и численных вычислений в области статистики. Позволяет строить очень красивые графики – иногда красивее, чем в Excel! Состоит из языка, компилятора, отладчика и run-time окружения для построения графиков. Позволяет использовать скрипты. Распространяется по условиям GNU General Public License лицензии.

·         Singular – специализированный пакет для работы с полиномами, с коммутативными алгебрами, особенно может быть полезен в алгебраической геометрии и теории особенностей. Распространяется по условиям GNU General Public License лицензии.GNU General Public License лицензии.

В 2004 года команда разработчиков получила ISAAC 2004 Richard D. Jenks Memorial Prize за разработку выдающегося программного обеспечения в области систем компьютерной алгебры.

·         YACAS ("Yet Another Computer Algebra System") – разработчики на сайте пишут, что это система для символьных манипуляций с математическими объектами. Используется собственный язык и библиотека скриптов. Мне данный пакет понравился своей документацией – более 320 страниц – написанной понятнее, чем документация для некоторых коммерческих продуктов. Распространяется по условиям GNU General Public License лицензии.

Существует огромное количество и других математических программ с открытым кодом и ”почти” открытым кодом, которые не попали в этот обзор и которые неспециалисту достаточно трудно найти в сети. Среди них CoCoA, Regina, Snappea, Geomview, Mathomatic, Euler, SciLab, Magma, Crack  и другие. Среди российских разработок  отмечу систему В.В.Монахова – BARSIC (http://barsic.spbu.ru/index_r.html) которая уже упоминалось на этой конференции.

В качестве отдельного примера мне бы хотелось привести программу Crack моего друга Thomas Wolf’a (http://citeseer.ist.psu.edu/462728.html), основной целью которой является решение систем переопределенных алгебраических и дифференциально-алгебраических уравнений. Для решения подобных систем используются самые современные алгоритмы, которые еще долго не будут реализованы в коммерческих продуктах, таких как Maple и Mathematica просто в силу того, что использование этих алгоритмов требует специальных знаний и опыта.

На примере систем CoCoA, Crack и других специализированных систем можно сделать заключение – существование огромного количества систем символьных вычислений с открытым кодом позволяет современному ученому достаточно эффективно решать поставленные перед ним задачи. Очевидными недостатками таких систем является отсутствие широкой рекламы возможностей данных систем и, как правило, довольно убогий интерфейс. В силу этого, реализуемая в настоящее время инициатива разработчиков SAGE, по объединению open-source проектов может привести к созданию единой достаточно функциональной open-source системы символьных вычислений. Нам же остается надеяться, что создание единой системы не приведет к созданию громоздкой системы, которая утратит свою гибкость и потенциал развития.